We often want to finetune base LLMs to use them on downstream tasks. However, it is difficult to finetune them since they contain billions of parameters and we also need to have a huge amount of memory to store both the model weights and the gradients for each weight. Using LoRA allows us to finetune with a lot fewer parameters.
LoRA freezes the original model weights during finetuning and instead adds a separate set of weights to train. After finetuning, these set of weights represent the differences we need to add to the pretrained parameters to make the model better for the finetuning task. At inference, you just load up the original weights + the updates and you still have the same number of parameters at inference.
LoRA is able to train fewer weights than the original weights of the model by decomposing the weight matrices into their low-rank decompositions which use fewer parameters while still approximating the full matrices.
Rank of a matrix
The rank of a matrix is the number of linearly independent columns in the matrix.
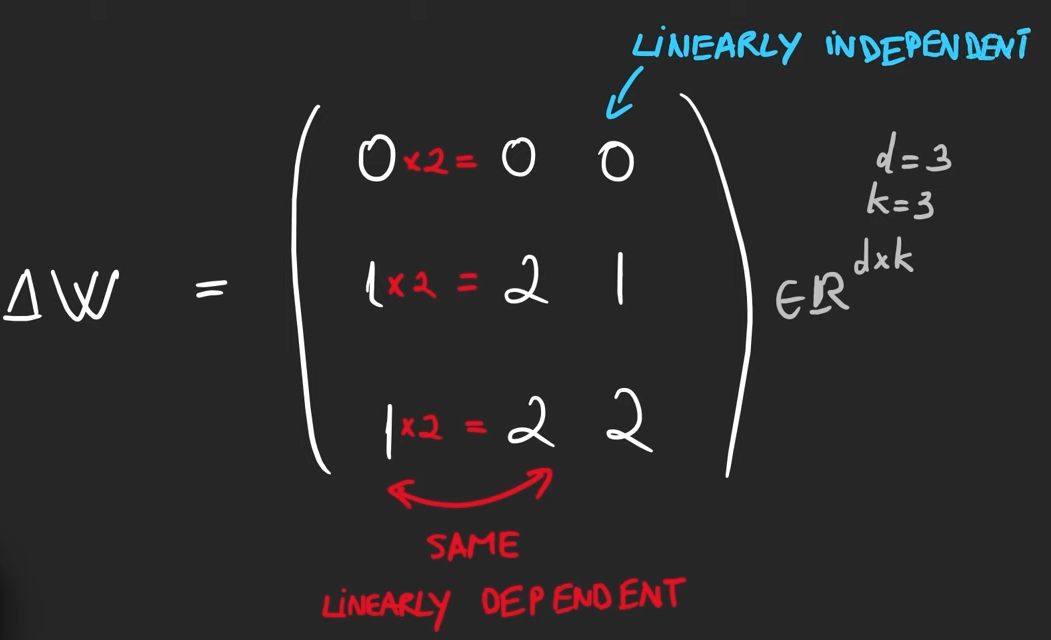A column is linearly independent if you can’t create it from a combination of the other columns in the matrix.
Low rank decomposition
LoRA’s idea is that you don’t need to optimize the full rank of the matrices. Instead, you can do a low-rank decomposition as representing the weights as a composition of two matrices ( and in the diagram below):
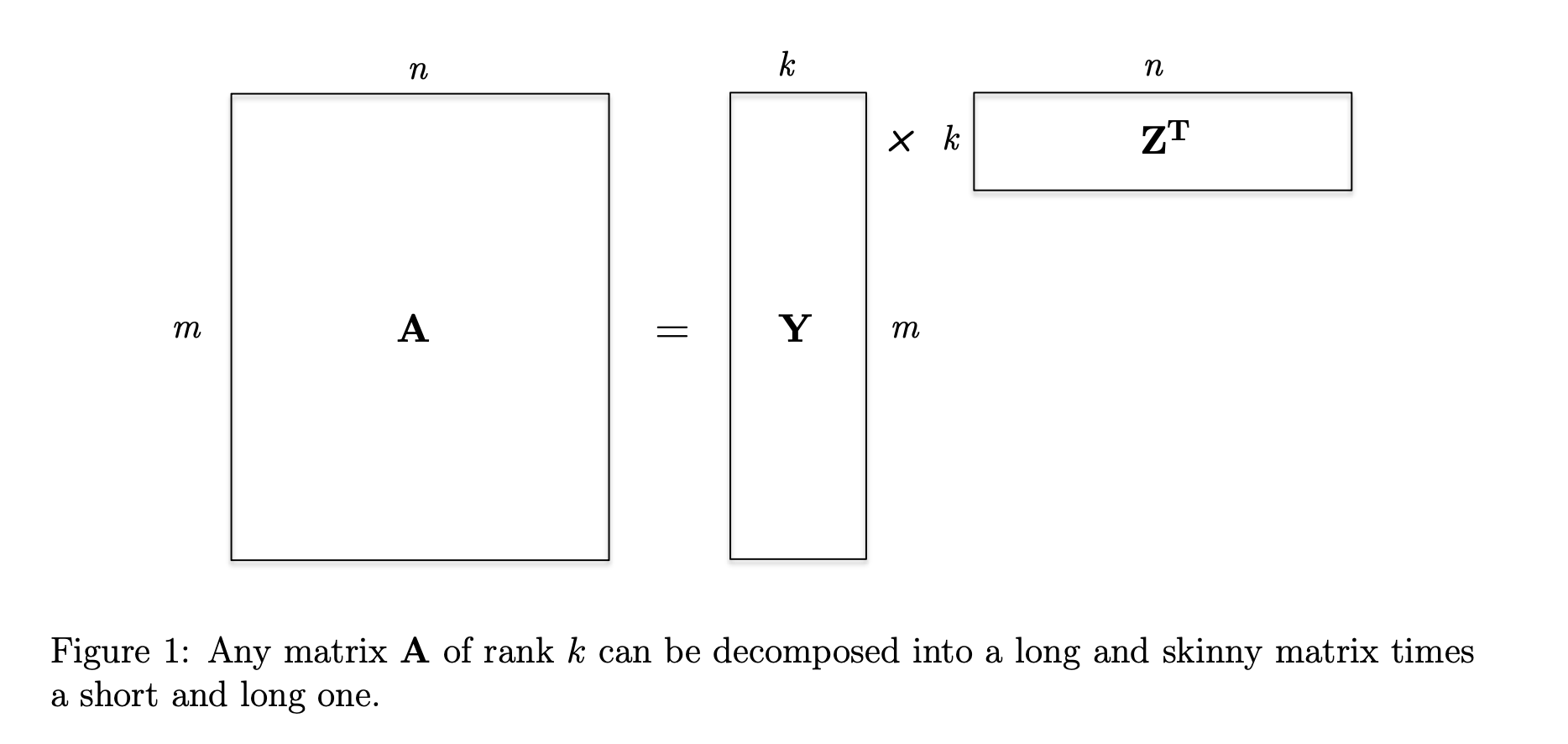
You can represent a matrix of size with rank by two matrices of size and . Instead of needing parameters, you just need parameters which is much smaller if the rank of the matrix is lower than the number of columns in it. For example, a matrix with rank 4 will have parameters but only parameters. Note: if the rank is not much lower than the number of columns, you don’t see a saving of parameters:
# ROWS = 10, COLS = 12
Rank=1: Parameters=22
Rank=2: Parameters=44
Rank=3: Parameters=66
Rank=4: Parameters=88
Rank=5: Parameters=110
Rank=6: Parameters=132
Rank=7: Parameters=154
Rank=8: Parameters=176
Rank=9: Parameters=198
Rank=10: Parameters=220
Rank=11: Parameters=242
Rank=12: Parameters=264
Note
The matrix allows us to shrink the dimensionality of to just the linearly independent columns and then the matrix allows us to recover the original number of columns of .
LoRA’s approach
LoRA’s learned weight differences () are approximated by two matrices () and ( where is the rank of .
is initialized from a Gaussian distribution and is initialized to and then you let backprop decide the parameter updates.
Instead of tuning the large matrix , you finetune the smaller weight matrices and .
After you find , you add these deltas to the original weights to get the final weights.
How to choose the rank?
The rank is a hyper-parameter and it seems even using rank = 1 can get good results. You can get away with very low ranks even if you end up losing a bit of information in your low rank decomposition. GitHub Post
LoRA vs. Adapter Modules
Adapters add small learnable layers throughout the network that update the behavior of the model by finetuning. They are very compute efficient but large models are often parallelized on hardware. Adapter modules need to be processed sequentially.
LoRA vs. Prefix Tuning
Instead of manually choosing the right words to prompt the model, you use input vectors that are concatenated to the prompt and then tune these vectors using backprop until the model delivers the correct answer.
Instead of using words to prompt the model:
you use input vectors that don’t stand for any words in particular:
The issue with prefix tuning is it occupies part of the sequence length and reduces the size of the effective input. It is also difficult to optimize and the number of trainable parameters is hard to choose.