Softmax

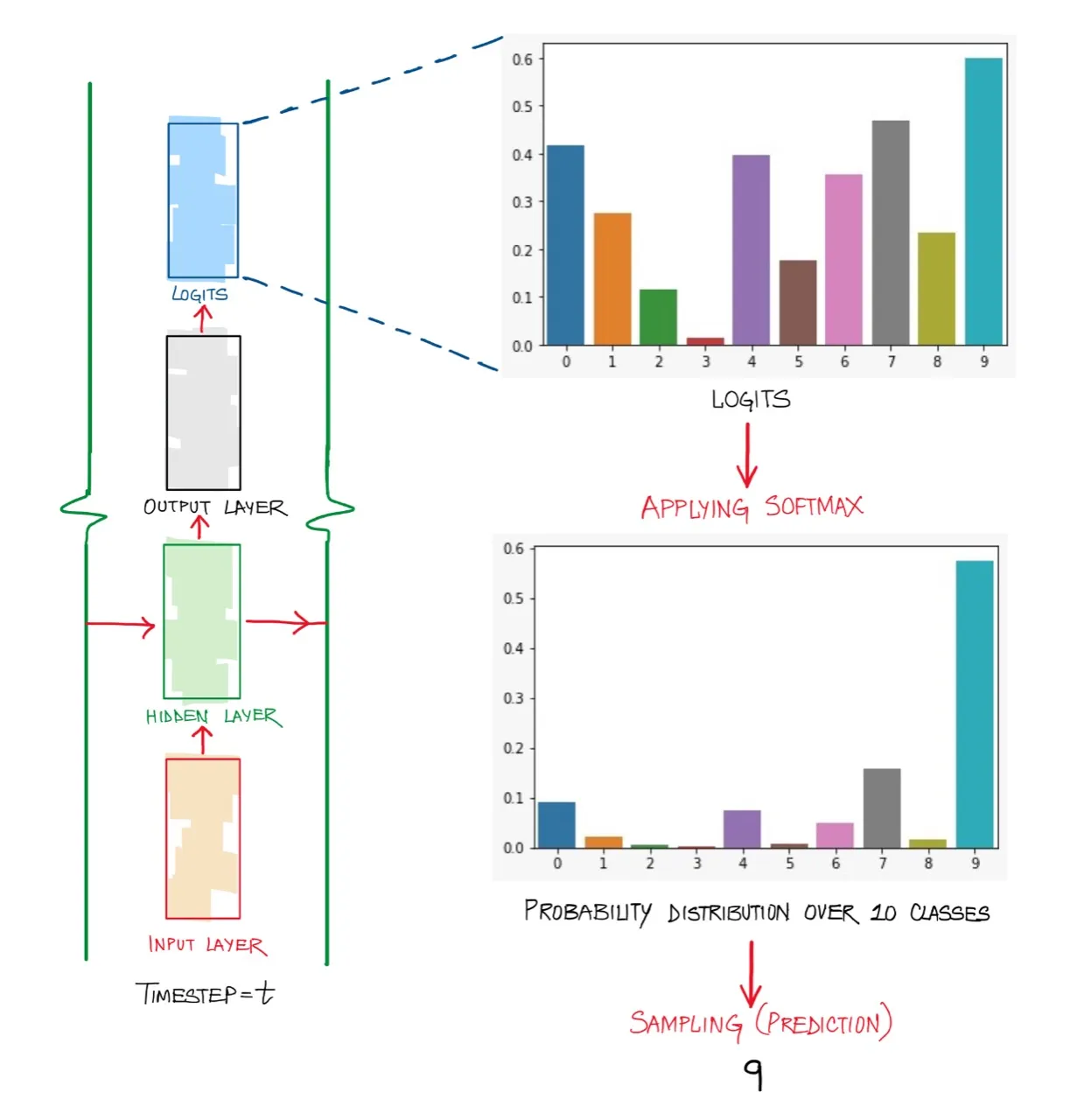
Softmax is often used to normalize the logits from a model (outputs from the last layer) so that they all lie between $[0,1]$ and sum to 1. A visualization can be seen below:

Source

When to use softmax vs. sigmoid?

Use softmax for multiple-class prediction and Sigmoid for binary prediction. The two are equivalent for binary classification. See the bottom of the page for more details.

Softmax Function §

The softmax function is used to convert the raw scores given by the classifier (aka logits) to normalized scores that add up to 1. Softmax has the nice property that it can take in negative values and ensure the output is positive and that all the outputs add up to 1 (converts everything to probabilities).

It is called softmax because it is like a softer version of a max function. It will give a higher probability to the larger value.

$${\hat{y}}_c=\frac{e^{z_c}}{{\sum }_j{e}^{z_j}}$$

Calculation:

1. First you take the exponential of the raw scores $z_c$ with $e^{z_c}$. This ensures all values are positive and non-zero. The new values are $e^{z_j}$.
2. You then sum up all the positive scores ${\sum }_j{e}^{z_j}$ and divide the positive scores calculated in step 1, $e^{z_j}$, by the sum of the scores, to normalize them to add up to 1.

PyTorch Example:

m = nn.Softmax(dim=1)
input = torch.randn(2, 3)
output = m(input)

When to use Sigmoid vs. softmax §

If you have a multi-label classification problem = there is more than one “right answer” = the outputs are NOT mutually exclusive, then use a sigmoid function on each raw output independently. The sigmoid will allow you to have high probability for all of your classes, some of them, or none of them. Example: classifying diseases in a chest x-ray image. The image might contain pneumonia, emphysema, and/or cancer, or none of those findings.

If you have a multi-class classification problem = there is only one “right answer” = the outputs are mutually exclusive, then use a softmax function. The softmax will enforce that the sum of the probabilities of your output classes are equal to one, so in order to increase the probability of a particular class, your model must correspondingly decrease the probability of at least one of the other classes. Example: classifying images from the MNIST data set of handwritten digits. A single picture of a digit has only one true identity - the picture cannot be a 7 and an 8 at the same time.

For binary classification, sigmoid and softmax are the same: Using Sigmoid with dummy encoded output (one binary column) vs using softmax with two one-hot encoded columns (one of the columns is equal to one, the other is zero) is mathematically equivalent and should give same results. Source.

Softmax with temperature scaling §

You can add in a scaling term $t$ which divides the logit tensor and then applies softmax to the result. The scale of temperature controls the smoothness of the output distribution. As $t\to \infty$, the distribution becomes more uniform, thus increasing the uncertainty. Contrarily, when $t\to 0$, the distribution collapses to a point mass.

$${\hat{y}}_c=\frac{e^{\frac{z_c}{t}}}{{\sum }_j{e}^{\frac{z_j}{t}}}$$

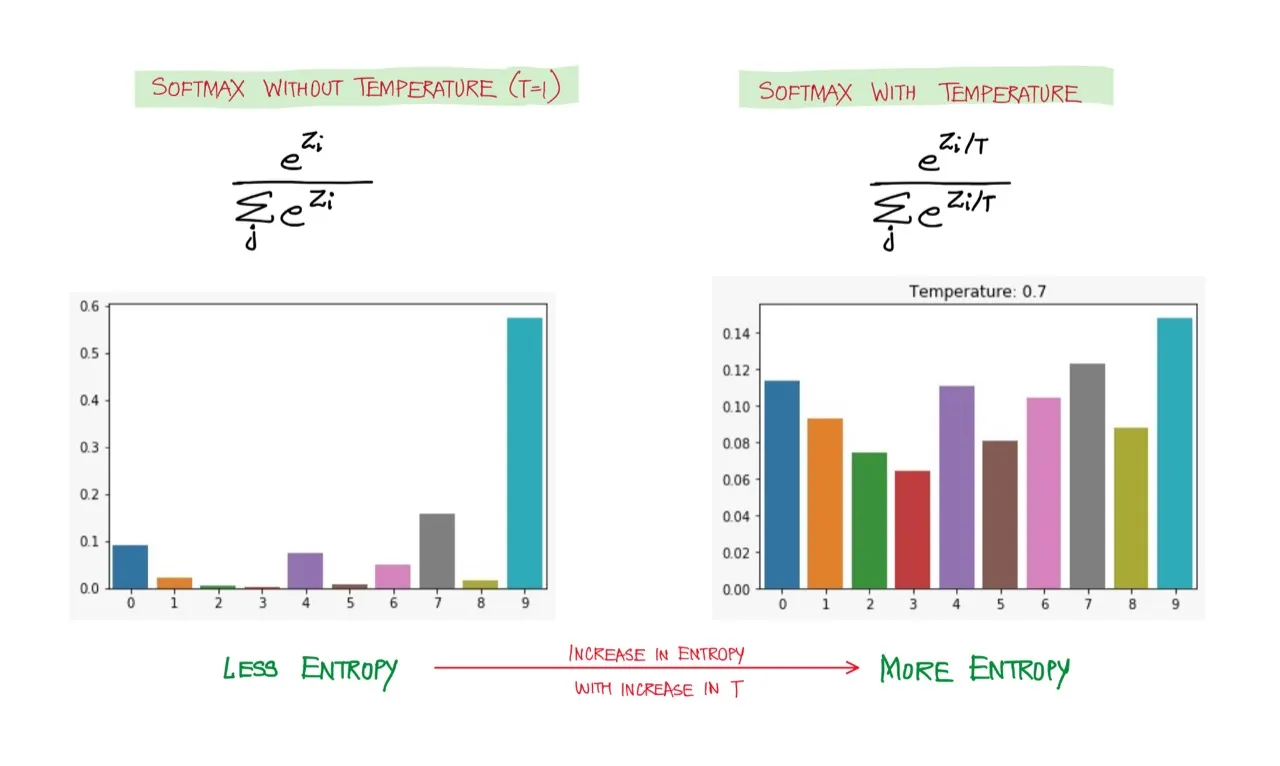
Visualizing the Effects of Temperature Scaling. Each word gets equal probability as the Temperature increases. Source

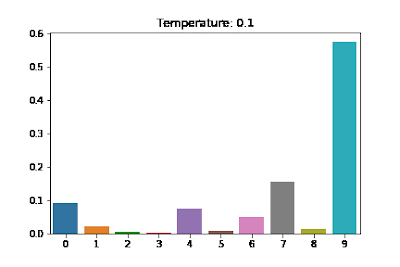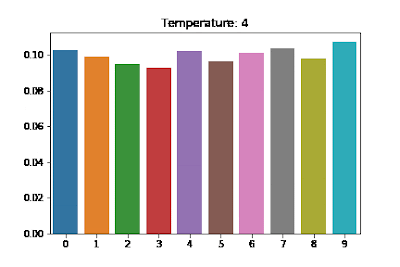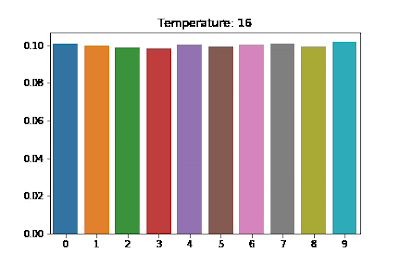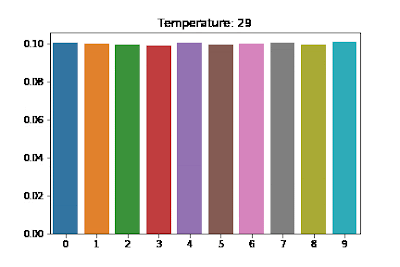
Softmax Temperature Scaling for Controlling LLM Output §

At each time step in the decoding phase (creating the full output sequence from a LLM), we need to predict a token, which is done by sampling from a softmax distribution (over the set of all possible tokens) using a sampling technique.

If you use sampling then you will select from the probability distribution over all possible tokens at each step. If you want the responses to be more creative and interesting, you can use temperature scaling to make the peak of the distribution less sharp (use a higher temperature) which results in you being more likely to pick words besides the absolute most likely candidate. If you want the responses to be very safe, you can decrease the temperature and as $t\to 0$, you will end up approaching just a greedy sampling approach where you always pick the most likely next token.