DETR

Description from DINO about DETR

DETR is a novel Transformer-based detection algorithm. It eliminates the need of hand-designed components like anchors and NMS which can’t be end-to-end optimized and achieves comparable performance with optimized classical detectors like Faster RCNN. Different from previous detectors, DETR models object detection as a set prediction task and assigns labels by bipartite graph matching. It leverages learnable queries to probe the existence of objects and combine features from an image feature map, which behaves like soft ROI pooling.

Despite its promising performance, the training convergence of DETR is slow and the meaning of queries is unclear.

DETR's 50 line PyTorch implementation doesn't exactly match the actual source code used

“This code uses learnt positional encodings in the encoder instead of fixed, and positional encodings are added to the input only instead of at each transformer layer”

Overview §

• DETR is a new method that treats object detection as a direct set prediction problem.
• They remove hand-designed components like Non-maximum Suppression, Anchors, and regressing bounding boxes that explicitly encode our prior knowledge about the task.
• Uses a set-based global loss that forces unique predictions via bipartite matching (a bipartite graph is a graph whose vertices can be divided into two disjoint and independent sets U and V, that is every edge connects a vertex in U to one in V.) and a transformer encoder-decoder architecture.
• Predicts set of predictions in parallel (non-autoregressive) given a fixed small set of learned object queries.

Benefits of transformers:

• Self-attention mechanisms of transformers model all pairwise elements between elements in a sequence which is useful for removing duplicate predictions.
• Transformers have a good trade-off between computational cost and the ability to perform the global computations required for set prediction.

Architecture §

The DETR architecture consists of three parts: a CNN backbone to extract features, an encoder-decoder transformer, and a feed forward network to make the final detection prediction.

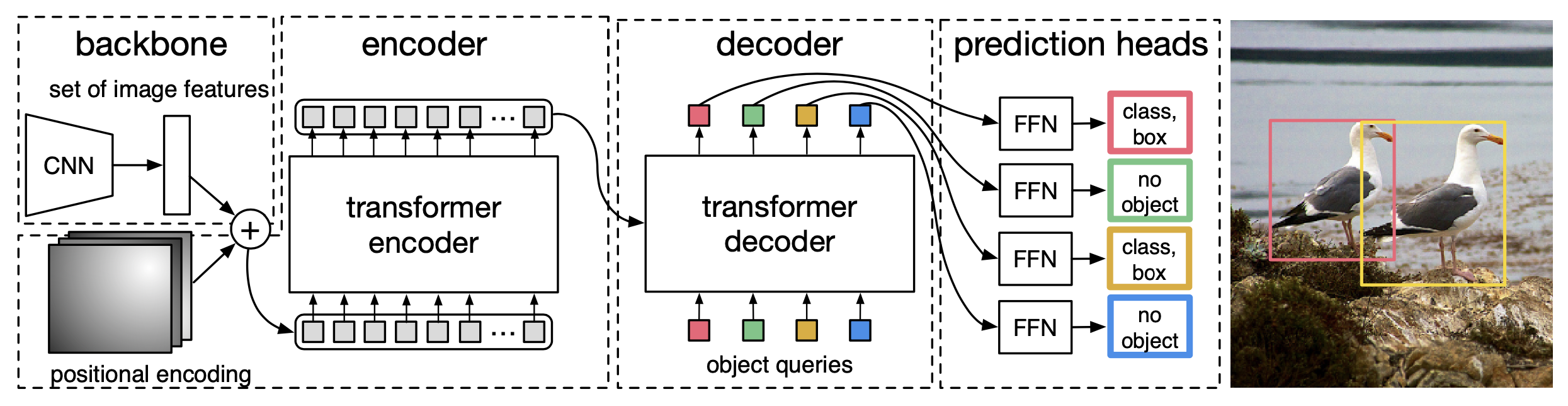
Transclude of DN-DETR#detr-architecture

Backbone: §

• You pass your image ($x_{\mathrm{img}}\in {\mathbb{R}}^{3\times H_0\times W_0}$) to a CNN which gives you a set of image features ($f\in {\mathbb{R}}^{C\times H\times W}$ where $C=2048$ and $H,W=\frac{H_0}{32},\frac{W_0}{32}$).

Transformer §

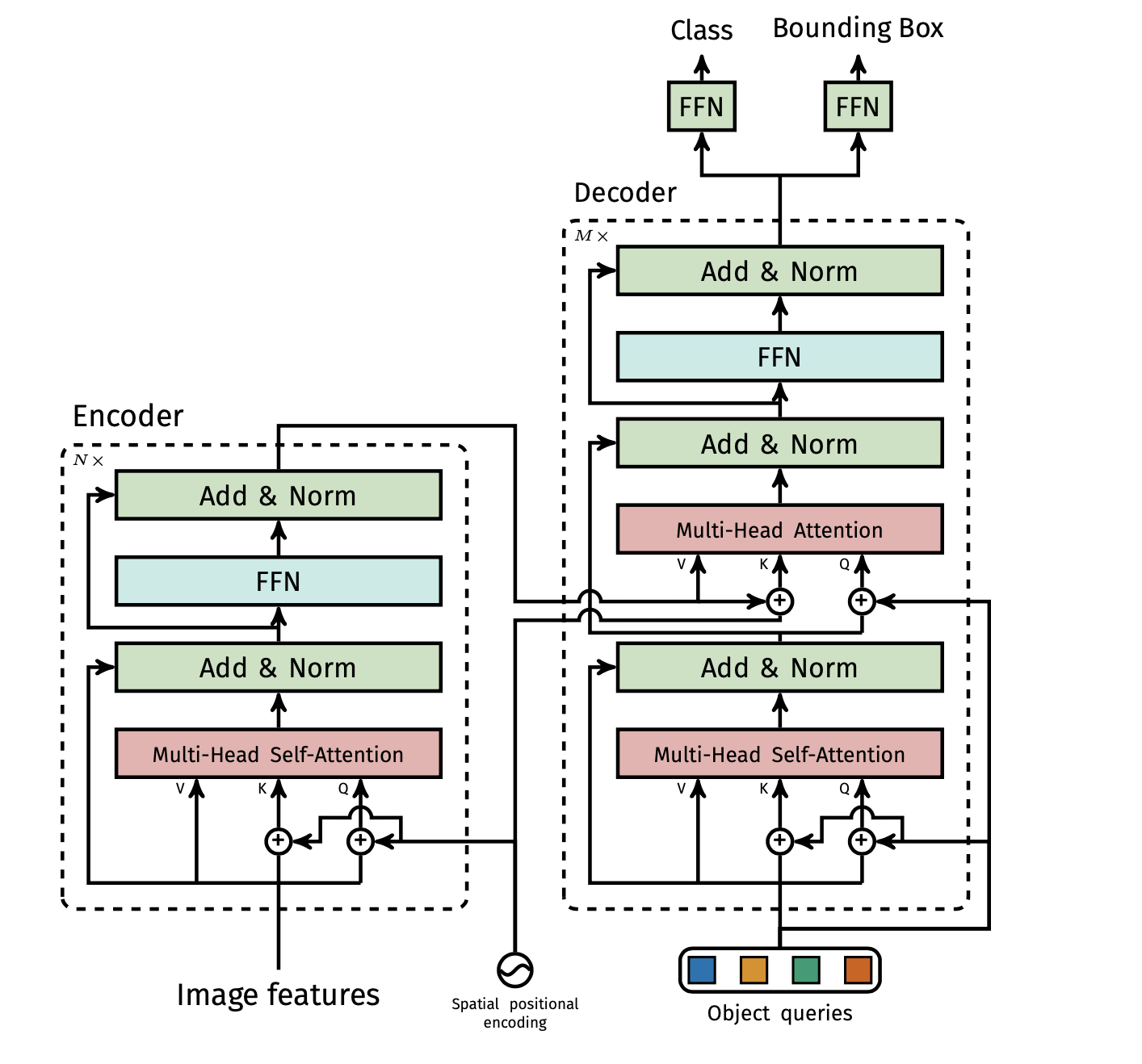
Transformer encoder: §

• Reduce the channel dimension via a 1x1 convolution from $C$ to $d$ creating a new map $z_0\in {\mathbb{R}}^{d\times H\times W}$.
• The encoder expects a sequence as input, so the spatial dimensions of $z_0$ are collapsed which gives a $d\times HW$ feature map and you get $d$ tokens.
• You add a positional embedding to each image feature token.
• You then pass the tokens to a transformer encoder which uses self-attention and gives a set of outputs where each output has attended to all other inputs.

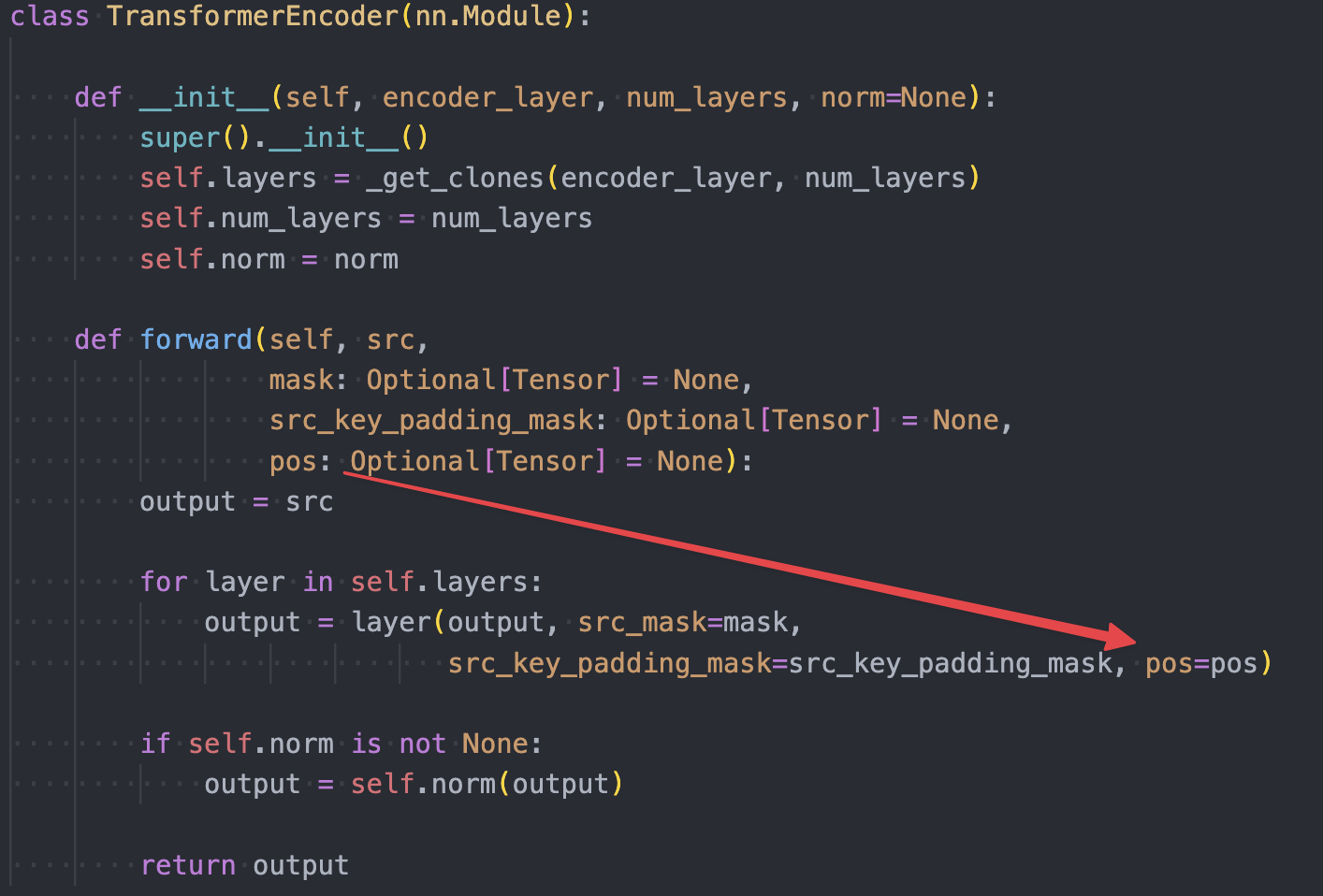
The features from the CNN backbone (src) are passed to the transformer encoder with spatial positional encoding (pos). The positional encoding is added to the queries and keys at every multi-head self-attention layer (not just the first one as is typically done for Transformers).

Transformer decoder: §

• You pass the output tokens from the encoder to a transformer decoder which then uses regular attention (not self-attention) where the keys and values come from the outputs of the encoder and the queries are learnt object queries.
• The $N$ object queries need to be different in order to produce different results since the decoder is permutation-invariant (if you had the same object query shifted in a different position it would still yield the same result).
• Multiple layers of the decoder are needed since a single decoding layer of the transformer is not able to compute any cross-correlations between the output elements, and thus it is prone to making multiple predictions for the same object. This is because a single layer will take in the output tokens from the encoder for keys/values and the queries are learnt object queries. Additional decoder layers are needed to cross-correlate between the output tokens to make sure they are unique.

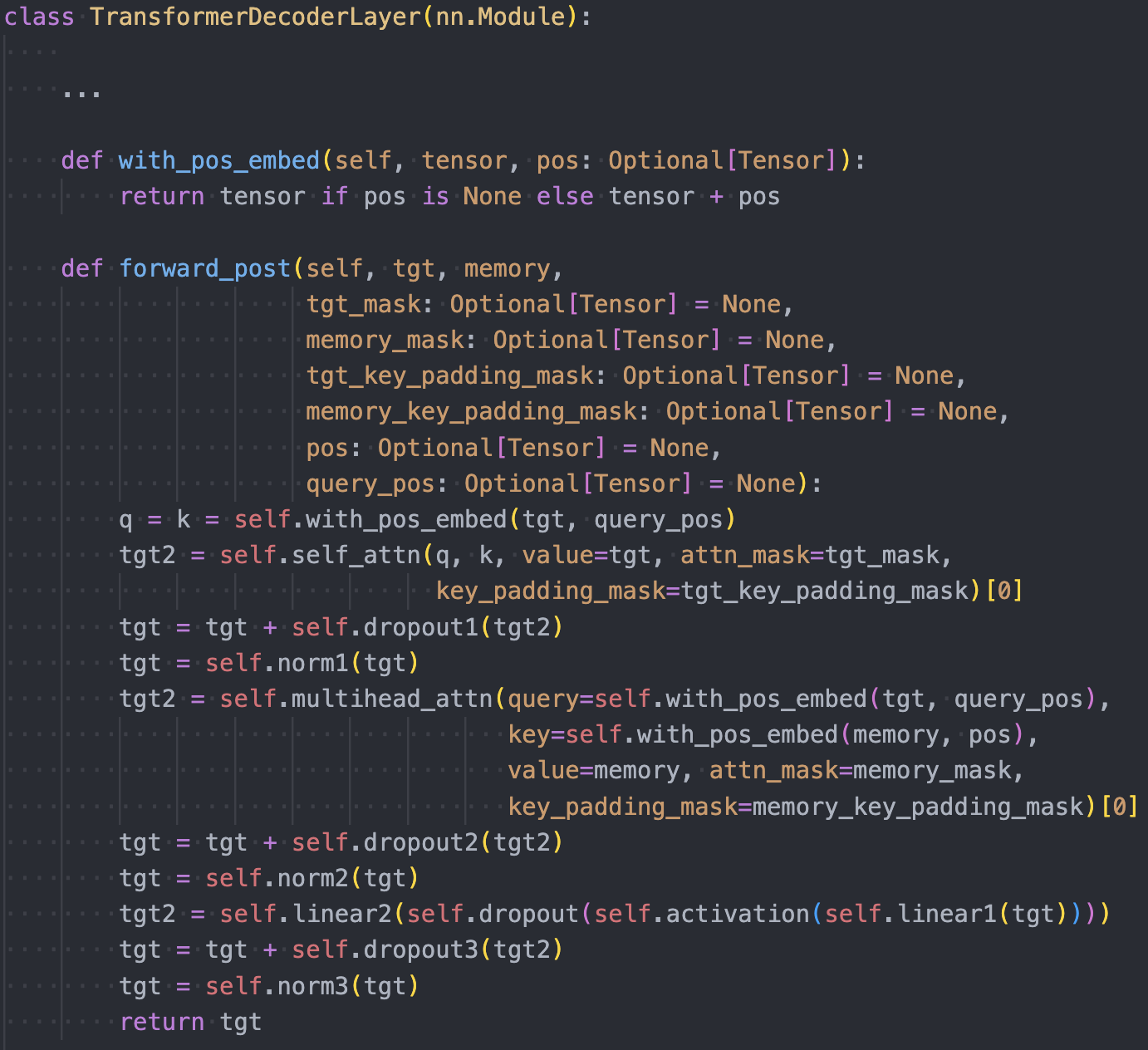Above is the source code for DETR’s TransformerDecoderLayer.

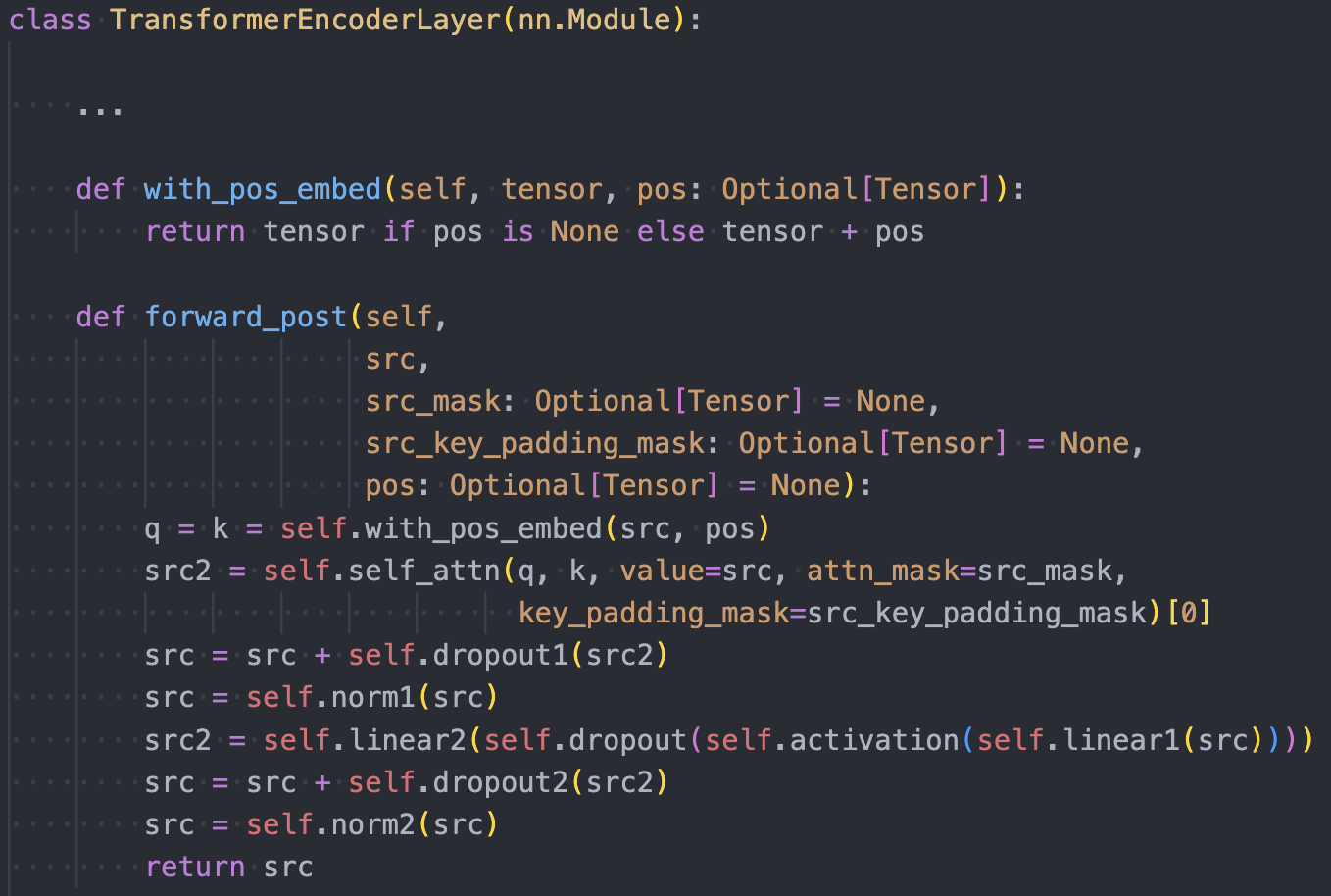
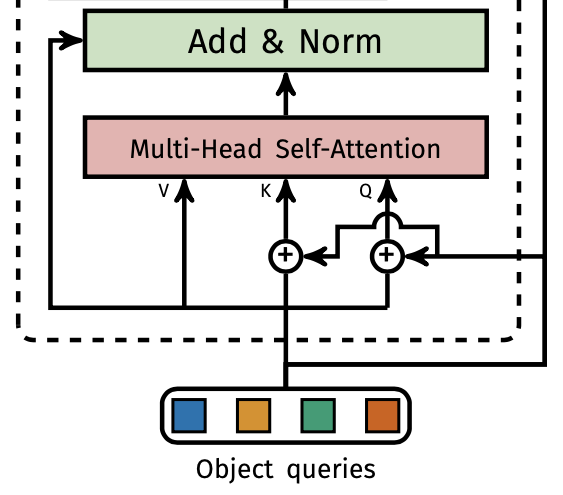Self-Attention: The decoder first computes self-attention on the incoming sequence (this step can be skipped for the first self-attention layer in the first decoder, but the code seems not to skip it). This is done via: where the sequence is used to create the queries, keys, and values. The positional embeddings (pos) are added to just the queries and keys.

Multi-Head Cross-Attention: The decoder then computes multi-head attention:

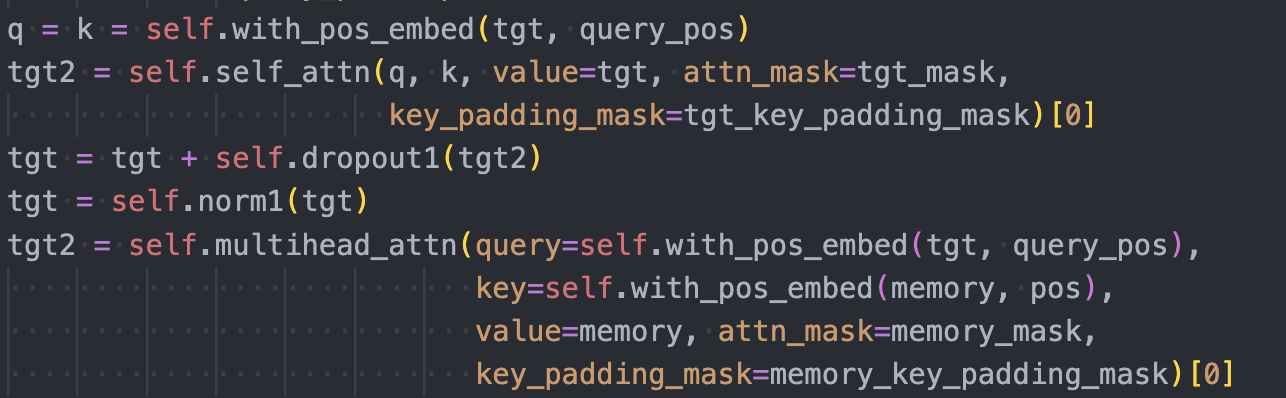
• The output of self-attention is tgt (after dropout, residual connection, and normalization).
• Queries come from tgt + query_pos (object queries).
• Keys come from memory (output of the encoder) + pos (positional encodings).
• Values come from memory

The below diagram shows the cross-attention within DETR’s transformer decoder:

Prediction feed-forward network (FFN) §

• The output embeddings are decoded independently by the FFN resulting in $N$ final predictions. Note that $N$ is a hyperparameter decided before-hand and is the number of output
• You have a MLP that predicts the normalized center coordinates, height, and width of the box with respect to the input image.
• You also have a linear layer that predicts the class label with a softmax function. There is an additional $\varnothing$ class that plays a similar role to the “background” class in standard object detection approaches.

def __init__():
    self.class_embed = nn.Linear(hidden_dim, num_classes + 1)
    self.bbox_embed = MLP(hidden_dim, hidden_dim, 4, 3)
 
def forward():
    hs = self.transformer(...)
    
    outputs_class = self.class_embed(hs)
    outputs_coord = self.bbox_embed(hs).sigmoid()

Source

Number of output embeddings

DETR infers a fixed-size set of $N$ predictions, in a single pass through the decoder, where $N$ is set to be significantly larger than the typical number of objects in an image. $N$ is different than the number of classes.

Direct Set Prediction §

• You need to avoid near-duplicate predictions.
• Most detectors use Non-maximum Suppression to address this issue, but direct set prediction is postprocessing-free. This requires inference schemes that model interactions between all predicted elements to avoid redundancy.
• A FC network is sufficient for constant size set prediction, but it is also expensive and doesn’t work for varying size sets.
• DETR uses a loss based on the Hungarian algorithm, to find a bipartite matching between ground-truth and prediction. This enforces permutation-invariance, and guarantees that each target element has a unique match. Having an unique matching allows predictions to be emitted in parallel.

Critical components:

1. Set prediction loss that forces unique matching between predicted and ground truth boxes.
2. The loss produces the optimal bipartite matching between predicted and ground truth objects, and then optimize object-specific (bounding box) losses.
3. An architecture that predicts (in a single pass) a set of objects and models their relation.

Object detection set prediction loss §

• DETR predicts a fixed-size set of $N$ predictions in a single pass through the decoder.
• $N$ is set to be much larger than the typical number of objects in an image and if there are fewer than $N$ objects, the predicted set will be padded with $\varnothing$ (no object).
• The loss produces an optimal bipartite matching between predicted and ground truth objects, and then optimize the object-specific (bounding box) losses.

To find the bipartite matching between the two sets (ground truth $y$) and the set of $N$ predictions $\hat{y}={\left\{{\hat{y}}_i\right\}}_{i=1}^N$ ), they find a permutation of $N$ elements ($\sigma \in {\mathfrak{S}}_N$) with the lowest cost (they check every possible ordering of elements and find the one that minimizes the cost): $\hat{\sigma }=\underset{\sigma \in {\mathfrak{S}}_N}{\mathrm{argmin}}{\sum }_i^N{\mathcal{L}}_{\mathrm{match}}\left(y_i,{\hat{y}}_{\sigma (i)}\right)$ where ${\mathcal{L}}_{\mathrm{match}}\left(y_i,{\hat{y}}_{\sigma (i)}\right)$ is a pair-wise matching cost between ground truth $y_i$ and a prediction with index $\sigma (i)$. The optimal assignment is calculated with the Hungarian Algorithm using ${\mathcal{L}}_{\mathrm{match}}$.

$\sigma$ is the particular permutation of indices currently being looked at.

Note ${\mathcal{L}}_{\mathrm{match}}$ vs. ${\mathcal{L}}_{\text{Hungarian}}$

${\mathcal{L}}_{\mathrm{match}}$ is the cost used by the Hungarian Algorithm to decide the best match between the predictions and the ground truth.

${\mathcal{L}}_{\text{Hungarian}}$ is the loss describing how well the models predictions match the ground truth boxes they’ve been matched to.

The matching cost uses the probabilities of the class predictions while the Hungarian loss uses log-probabilities. The matching cost uses the raw probabilities because this makes the class prediction term commensurable to ${\mathcal{L}}_{\text{box }}$ which led to better empirical results.

Matching cost: §

• The matching cost takes into account both the class prediction and the similarity of predicted and ground truth boxes.
• Each element $i$ of the ground truth set can be seen as $y_i=\left(c_i,b_i\right)$ where $c_i$ is the target class label (which may be $\varnothing$) and $b_i\in [0,1{]}^4$ is a vector that defines the ground truth box center coordinates and its height and width relative to the image size.
• For the prediction with index $\sigma (i)$ the probability of class $c_i$ is ${\hat{p}}_{\sigma (i)}\left(c_i\right)$ and the predicted box is ${\hat{b}}_{\sigma (i)}$.

The matching loss is defined as: ${\mathcal{L}}_{\mathrm{match}}\left(y_i,{\hat{y}}_{\sigma (i)}\right)=-1_{\left\{c_i\ne \varnothing \right\}}{\hat{p}}_{\sigma (i)}\left(c_i\right)+1_{\left\{c_i\ne \varnothing \right\}}{\mathcal{L}}_{\mathrm{box}}\left(b_i,{\hat{b}}_{\sigma (i)}\right)$ where $1$ is the indicator function.

• If the ground truth label for prediction $i$ is not no object ($c_i\ne \varnothing$) then this will be -1 * the probability that the predicted belongs to class $c_i$. The higher the predicted probality for the ground truth class, the lower the overall loss will be.
• You then add 1 * the bounding box loss between the ground truth and predicted boxes (if the prediction is not no object).
• They don’t use log-probability for the class prediction term to make it commensurable to ${\mathcal{L}}_{\text{box }}$ and better empircal performance is found.

Bounding box loss ${\mathcal{L}}_{\text{box }}$ §

• Recall: the bounding box values predicted are normalized center coordinates, height, and width.
• DETR makes bounding box predictions directly (vs. adjustments to initial predictions) so it is hard to use L1 Loss since it will have different scales for large and small boxes even if their relative errors are similar.

To address the issue of using L1 loss alone, they use a linear combination of L1 loss and IoU loss that is scale-invariant: ${\mathcal{L}}_{\mathrm{box}}\left(b_i,{\hat{b}}_{\sigma (i)}\right)={\lambda }_{\text{iou }}{\mathcal{L}}_{\text{iou }}\left(b_i,{\hat{b}}_{\sigma (i)}\right)+{\lambda }_{\mathrm{L}1}{\Vert b_i-{\hat{b}}_{\sigma (i)}\Vert }_1$ where ${\lambda }_{\mathrm{iou}},{\lambda }_{\mathrm{L}1}\in \mathbb{R}$ are hyperpameters. The L1 and IoU losses are normalized by the number of objecs inside the batch.

The full form of the matching loss (with ${\mathcal{L}}_{\text{box }}$ expanded) is: ${\mathcal{L}}_{\mathrm{match}}\left(y_i,{\hat{y}}_{\sigma (i)}\right)=-1_{\left\{c_i\ne \varnothing \right\}}{\hat{p}}_{\sigma (i)}\left(c_i\right)+1_{\left\{c_i\ne \varnothing \right\}}{\lambda }_{\text{iou }}{\mathcal{L}}_{\text{iou }}\left(b_i,{\hat{b}}_{\sigma (i)}\right)+{\lambda }_{\mathrm{L}1}{\Vert b_i-{\hat{b}}_{\sigma (i)}\Vert }_1$

Hungarian Loss §

After matching pairs using the Hungarian Algorithm with costs calculated with the matching cost (${\mathcal{L}}_{\text{match }}\left(y_i,{\hat{y}}_{\sigma (i)}\right)$), the next step is to compute the Hungarian loss for these matched pairs (the loss describing how close the predictions are to the ground truth). This is defined as a linear combination of a negative log-likelihood for class prediction and a box loss.

${\mathcal{L}}_{\text{Hungarian }}(y,\hat{y})={\sum }_{i=1}^N\left[-\log {\hat{p}}_{\hat{\sigma }(i)}\left(c_i\right)+1_{\left\{c_i\ne \varnothing \right\}}{\mathcal{L}}_{\mathrm{box}}\left(b_i,{\hat{b}}_{\hat{\sigma }}(i)\right)\right]$

• This will compute the loss based on the ground truth ($y$) and predictions ($\hat{y}$). It will use the optimal matching pair assignments based on the matching loss ($\hat{\sigma }$).
• This will sum up $\left[-\log {\hat{p}}_{\hat{\sigma }(i)}\left(c_i\right)+1_{\left\{c_i\ne \varnothing \right\}}{\mathcal{L}}_{\mathrm{box}}\left(b_i,{\hat{b}}_{\hat{\sigma }}(i)\right)\right]$ for all $N$ predictions.
• The log of a number less than 1 is negative and $\log (0.01)=-2$ and $\log (0.99)=-0.0043$. $-\log {\hat{p}}_{\hat{\sigma }(i)}\left(c_i\right)$ will be close to 0 if the predicted probability is close to 1 and it will be close to 1 if the predicted probability is close to 0.
• DETR down-weights the log-probability term when $c_i=\varnothing$ to account for class imbalance.

Training §

• Transformers are typically trained with Adam or Adagrad optimizers with very long training schedules and dropout, and this is true for DETR as well.
• DETR is known for taking a long time to train.

Results §

• Performs better on larger objects (likely because of the non-local computations of the transformer).
• Has worse performance on small objects. Modern object detectors use multi-scale features where small objects are detected from high-resolution feature maps. DETR is unable to process high resolution feature maps bevuase the attention weight computation in the transformer encoder is quadratic w.r.t. the number of pixels (note the transformer decoder takes the output of the encoder as the keys, values to the multi-head attention, but the queries come from the object queries so the complexity isn’t quadratic w.r.t. the number of pixels).
• DETR takes a long time to train. This is likely because at initialization the attention modules cast nearly uniform attention weights to all pixels in the feature maps. It takes a long time to learn to focus on sparse meaningful locations.
• Achieves competitive results compared to Faster R-CNN on COCO.

DETR Panoptic Segmentation §

The paper added a panoptic head to predict a pixel-wise binary mask for whether a pixel inside a bounding box belonged to the corresponding class or not. They needed to use bounding boxes (couldn’t go directly to masks) since the Hungarian Algorithm required bounding boxes to calculate distances.

Analysis of DETR’s Panoptic Performance from Panoptic SegFormer

• DETR predicts the bounding boxes of things and stuff and combines the attention maps of the transformer decoder and the feature maps of ResNet to perform panoptic segmentation.
• Because the computational complexity of self-attention is squared with the length of the input sequence, the feature resolution of DETR is limited.
• It uses an FPN-style panoptic head to generate masks, which have poor boundary predictions (resolution is too low).
• It represents “stuff” with bounding boxes which may be suboptimal.