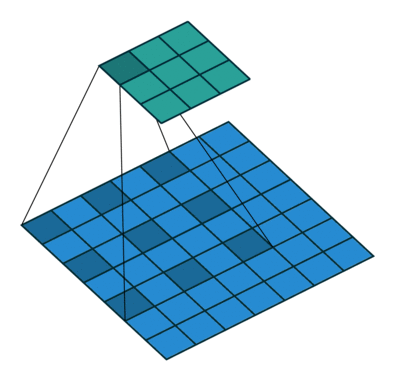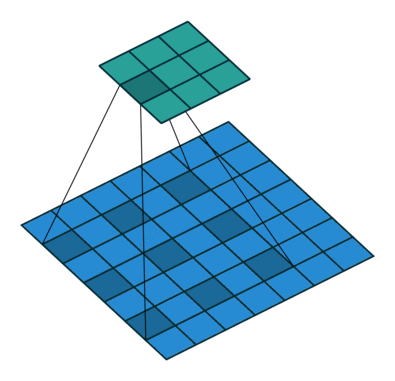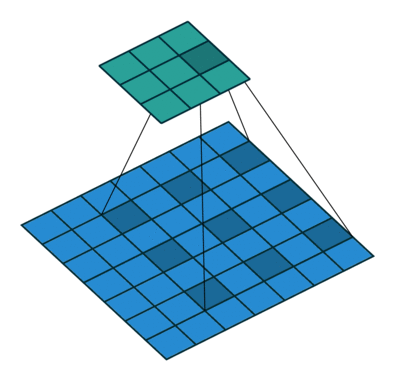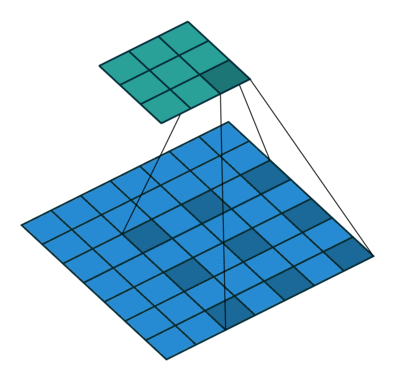
Dilated convolutions will expands the input by inserting holes between its consecutive elements. This results in a larger receptive field without needing additional layers or a larger filter size. On the left is a kernel with dilation=1 (the default) and on the right is a kernel with dilation=2. Both use a 3x3 kernel and the blue is the input and the green is the output. The FOV of the dilated kernel is closer to that of a 5x5 kernel.
As an example, in one dimension a filter w of size 3 would compute over input x the following: w[0]*x[0] + w[1]*x[1] + w[2]*x[2]. This is dilation of 0. For dilation 1 the filter would instead compute w[0]*x[0] + w[1]*x[2] + w[2]*x[4]; In other words there is a gap of 1 between the applications. Source.
Benefits of dilated convolution
You can keep the number of parameters and computation the same while increasing the FOV by increasing the dilation factor (aka “rate”).
Controlling spatial resolution of feature maps (DeepLab)
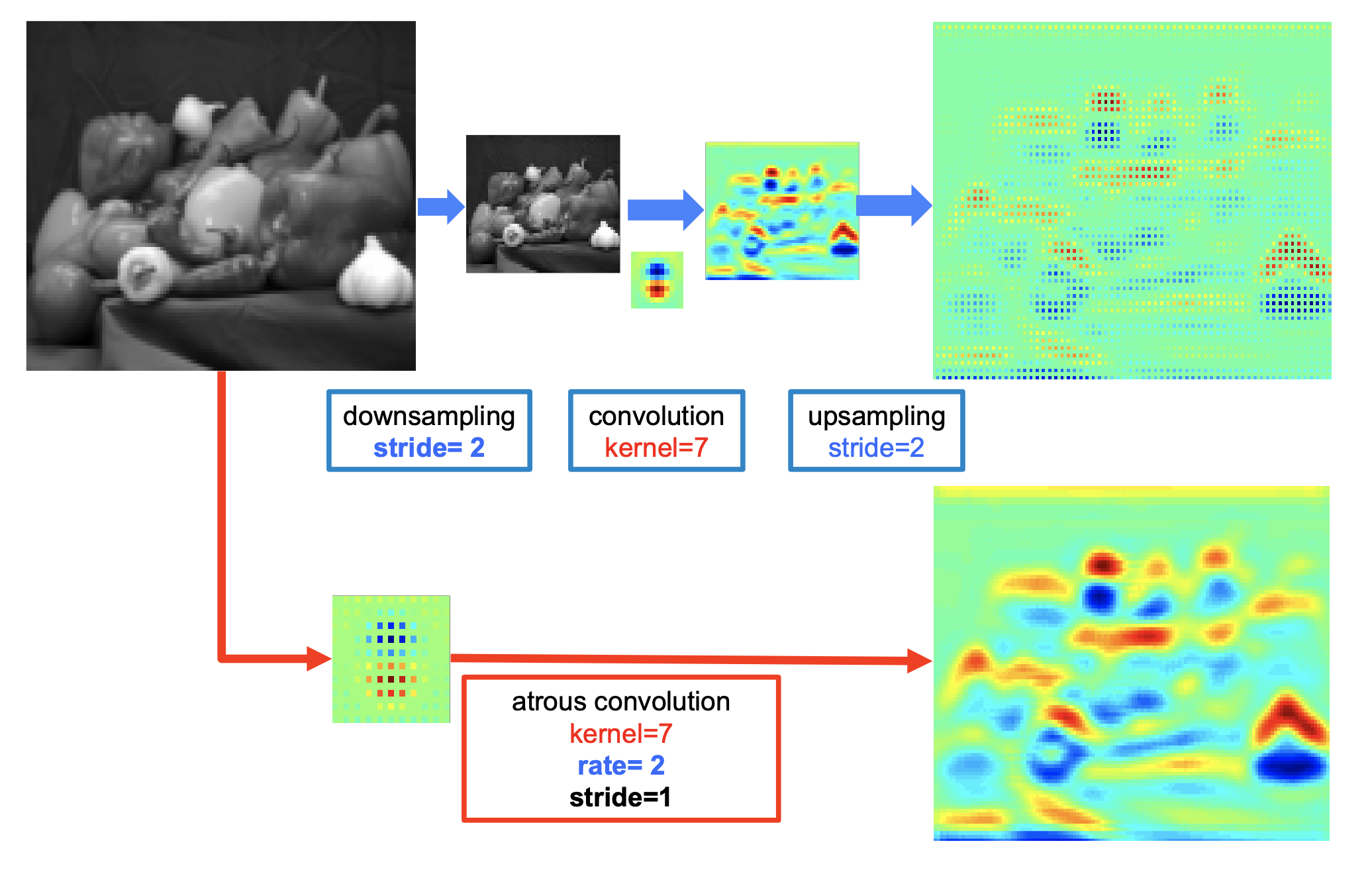In the above example, the top operation is as follows:
- Apply a dowsampling operation to reduce resolution by a factor of 2.
- Convolve with a filter (in this case the vertical ππGaussian derivative).
- Upsampling the resulting features by a factor of 2 to the original dimension. If you then implant the upsampled features into the original image coordinates, responses are only obtained at 1/4 of the image positions. Note: if you used bilinear interpolation then the upsampled features wouldn’t have the checkerboard appearance.
Instead of using a downsampling, convolution, and upsampling, you can use a single convolutional layer with a dilation factor of 2 to achieve the same results. You convolve the full resolution image with a filter “with holes”, in which you upsample the original filter by a factor of 2, and introduce zeros between filter values.
Although the effective filter size increases, we only need to take into account the non-zero filter values, hence both the number of filter parameters and the number of operations per position stay constant.
Dilated Convolutions for Segmentation
Dilated Convolutions are very beneficial for semantic segmentation since they allow for a larger receptive field without the need of more free parameters. UPSNet.
They are used extensively in the DeepLab series of architectures.