Note
The following are my notes from this article by Akbar Karimi
Beam Search is often used in autoregressive tasks such as machine translation where you first encode a sequence of words from the source language and then decode the intermediate representation into a sequence of words in the target language. In the decoding process, for each word in the sequence, there can be several options. This is where the beam search comes into play. At each time step you will only keep a fixed number of the best output sequences.
Beam search is an improved version of greedy search. It has a hyperparameter named beam size, 𝑘 . At time step 1, we select 𝑘 tokens with the highest conditional probabilities. Each of them will be the first token of 𝑘 candidate output sequences, respectively. At each subsequent time step, based on the 𝑘 candidate output sequences at the previous time step, we continue to select 𝑘 candidate output sequences with the highest conditional probabilities from possible choices. Source
It is a heuristic search algorithm that explores a graph by expanding the most promising node in a limited set. Beam search is an optimization of best-first search that reduces its memory requirements. Best-first search is a graph search which orders all partial solutions (states) according to some heuristic. But in beam search, only a predetermined number of best partial solutions are kept as candidates. It is thus a greedy algorithm.
Example
Let’s go through a simplified sample decoding process step by step. In this example, our heuristic function will be the probability of words and phrases that are possible in translation. First, we start with a token that signals the beginning of a sequence. Then, we can obtain the first word by calculating the probability of all the words in our vocabulary set. We choose (beam width) words with highest probabilities as our initial words {arrived, the}
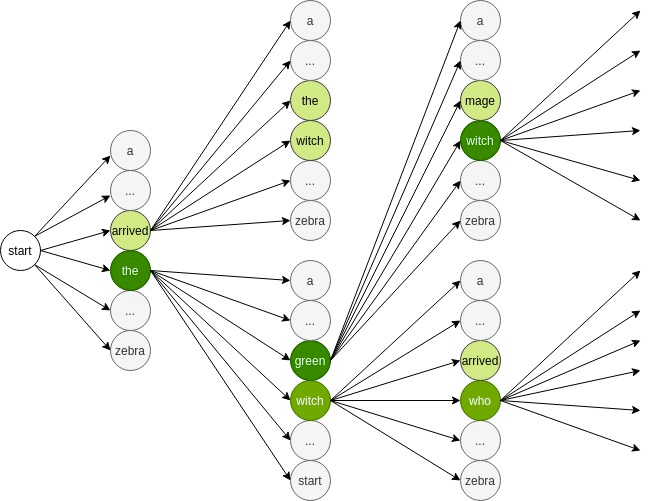
After that, we expand the two words and compute the probability of other words that can come after them. The words with the highest probabilities will be {arrived the, arrived witch, the green, the witch}. From these possible paths, we choose the two most probable ones ({the green, the witch}). Now we expand these two and get other possible combinations (the green witch, the green mage, the witch arrived, the witch who}). Once again, we select two words that maximize the probability of the current sequence ({the green witch, the witch who}). We continue doing this until we reach the end of the sequence. In the end, we’re likely to get the most probable translation sequence.
We should keep in mind that along the way, by choosing a small , we’re ignoring some paths that might have been more likely due to long-term dependencies in natural languages. One way to deal with this problem is to opt for a larger beam width.
Length normalization: Without some form of length-normalization regular beam search will favor shorter results over longer ones on average since a negative log-probability is added at each step, yielding lower (more negative) scores for longer sentences. GNMT