Lift, Splat, Shoot

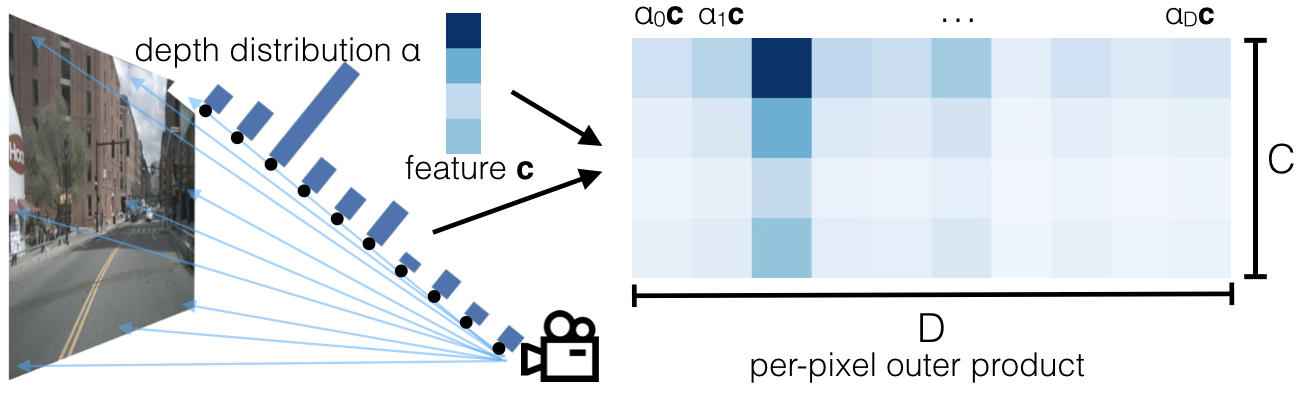
For each pixel, they predict a categorical distribution for $D$ bins where each bin has a step size of $\alpha$ and a context vector $\mathbf{c}\in {\mathbb{R}}^C$ (top left). Features at each point along the ray are determined by the outer product of $\alpha$ and $\text{c}$ (right).

Note that this diagram shows a single pixel only. The pixel has a feature vector $c$ and a depth distribution given by $\alpha$. At the cell (0, 2) you can see the outer product between the depth distribution and the feature is the highest so this pixel is darkest.

Lift: Latent Depth Distribution §

The following comes directly from the paper.

The first stage of our model operates on each image in the camera rig in isolation. The purpose of this stage is to lift each image from a local 2-dimensional coordinate system to a 3-dimensional frame that is shared across all cameras.

 The challenge of monocular sensor fusion is that we require depth to transform into reference frame coordinates but the depth associated to each pixel is inherently ambiguous. Our proposed solution is to generate representations at all possible depths for each pixel.

 Let $\mathbf{X}\in {\mathbb{R}}^{3\times H\times W}$ be an image with extrinsics $\mathbf{E}$ and intrinsics $\mathbf{I}$, and let $p$ be a pixel in the image with image coordinates $(h,w)$. We associate $|D|$ points $\{(h,w,d)\in {\mathbb{R}}^3\mid d\in D\}$ to each pixel where $D$ is a set of discrete depths, for instance defined by $\{d_0+\Delta ,...,d_0+|D|\Delta \}$. Note that there are no learnable parameters in this transformation. We simply create a large point cloud for a given image of size $D\cdot H\cdot W$. This structure is equivalent to what the multi-view synthesis community has called a multi-plane image except in our case the features in each plane are abstract vectors instead of $(r,g,b,\alpha )$ values.

 The context vector for each point in the point cloud is parameterized to match a notion of attention and discrete depth inference. At pixel $p$, the network predicts a context $\mathbf{c}\in {\mathbb{R}}^C$ and a distribution over depth $\alpha \in {△}^{|D|-1}$ for every pixel. The feature ${\mathbf{c}}_d\in {\mathbb{R}}^C$ associated to point $p_d$ is then defined as the context vector for pixel $p$ scaled by ${\alpha }_d$: ${\mathbf{c}}_d={\alpha }_d\mathbf{c}$

Explanation of $\alpha \in {△}^{|D|-1}$

The value $|D|-1$ comes from having $D$ points you are predicting and there being a step size of $\alpha$. Therefore, the $D$ points are separated by a total of $|D|-1$ deltas.

 Note that if our network were to predict a one-hot vector for $\alpha$, context at the point $p_d$ would be non-zero exclusively for a single depth $d^{\ast }$. If the network predicts a uniform distribution over depth, the network would predict the same representation for each point $p_d$ assigned to pixel $p$ independent of depth. Our network is therefore in theory capable of choosing between placing context from the image in a specific location of the bird’s-eye-view representation versus spreading the context across the entire ray of space, for instance if the depth is ambiguous.

 In summary, ideally, we would like to generate a function $g_c:(x,y,z)\in {\mathbb{R}}^3\to c\in {\mathbb{R}}^C$ for each image that can be queried at any spatial location and return a context vector. To take advantage of discrete convolutions, we choose to discretize space. For cameras, the volume of space visible to the camera corresponds to a frustum.